N 皇后问题
leetcode 第 51 题,N 皇后问题
题目描述
按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1: 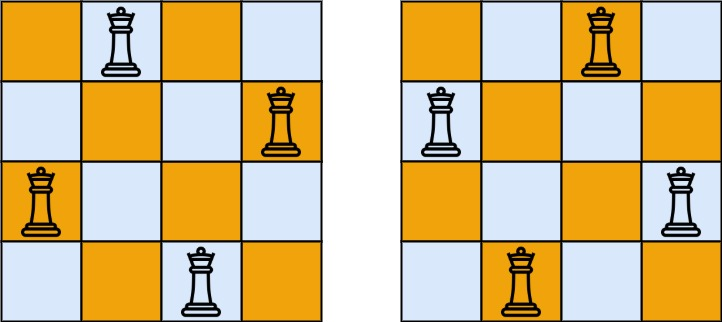
输入:n = 4 输出: ****[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:[["Q"]]
提示:
1 <= n <= 9
解题思路
- 每一行遍历,进行回溯递归
- 回溯递归的终止条件是,当第
n行的时候,所有的皇后都已经放置好了 - 遍历到的地方能否放置皇后的条件是:
- 每一行都不能有相同的皇后,我们是逐行遍历,不会出现重复
- 每一列都不能有相同的皇后
- 每一对角线都不能有相同的皇后(左上方和右上方)下方没有放置,不需要考虑
代码实现和注释
js
/**
* @param {number} n
* @return {string[][]}
*/
var solveNQueens = function (n) {
// 存储结果
const res = [];
// 每次结果的缓存
const board = Array.from({ length: n }, () => Array(n).fill("."));
// 回溯算法, 函数签名: 每一行遍历
function backtrack(row) {
// 判断是否遍历完成
if (row === n) {
res.push(board.map((a) => a.join("")));
return;
}
for (let col = 0; col < n; col++) {
// 如果不合法 本次树不递归
if (!isValid(row, col)) continue;
board[row][col] = "Q";
backtrack(row + 1);
board[row][col] = ".";
}
}
// 判断本次皇后位置是否合法
// 函数签名 行列,判断本次的位置是否合法
function isValid(row, col) {
// 判断左上角
for (let i = row, j = col; i >= 0 && j >= 0; i--, j--) {
// 左上方斜线有 Q 不合法
if (board[i][j] === "Q") return false;
}
// 判断方位 3
// 判断右上角
for (let i = row, j = col; i >= 0 && j < n; i--, j++) {
if (board[i][j] === "Q") return false;
}
// 判断正上方
for (let i = row; i >= 0; i--) {
if (board[i][col] === "Q") return false;
}
// 下方不需要判断 因为是从上往下放 下方还没有皇后
// 默认返回 true
return true;
}
backtrack(0);
return res;
};总结
N 皇后本质也是回溯,对每一列进行遍历,判断当前行哪个位置可放,然后递归回溯遍历下一行,遍历到最后一行,则是合法答案,放入结果数组。